Question

A double-slit diffraction pattern is formed on a distant screen. If the separation between the slits decreases, what happens to the distance between interference fringes? Assume the angles involved remain small.The distance between interference fringes remains the same.The effect cannot be determined unless the distance between the slits and the screen is known.The distance between interference fringes also decreases.The distance between interference fringes increases.

Answer 1

The distance between interference fringes increases.

Step-by-step explanation:

In a double-slit diffraction pattern, the angular position of the nth-maximum in the diffraction patter (measured with respect to the central maximum) is given by

`sin \theta = (n \lambda)/(d)`

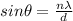
where

`\theta` is the angular position

`\lambda` is the wavelength

d is the separation between the slits

In this problem, the separation between the slits decreases: this means that d in the formula decreases. As we see, the value of
`sin \theta` (and so, also
`\theta`) is inversely proportional to d: so, if the d decreases, then the angular separation between the fringes increases.

So, the correct answer is

The distance between interference fringes increases.