Question

Simplify expression 49 with an exponent of 1/2

Answer 1

Answer: 7

Step-by-step explanation: To simplify
`49^(1/2)`, it's important to understand that an exponent of 1/2 means that we take the square root of the base. In other words,
`49^(1/2)` means the same thing as the square root of 49 or
`√(49)` and the square root of 49 is 7.

This means that
`49^(1/2)` is 7.

Answer 2

Hello!

The answer is:

The simplified form of the given expression is 7.

`49^{(1)/(2)}=\sqrt[2]{49^(1)}=\sqrt[2]{49}=7`

Why?

To simplify the given expression, we must remember the following property of roots:

`a^{(m)/(n)}=\sqrt[n]{a^(m) }`

We are given the expression:

`49^{(1)/(2)}`

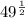
Which can be also written as:

`49^{(1)/(2)}=\sqrt[2]{49^(1)}=\sqrt[2]{49}`

Then, simplifying we have:

`\sqrt[2]{49}=7`

Hence, the simplified form of the given expression is 7.

Have a nice day!