Answer:
Both
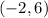 and
and
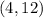 are solutions to the system.
are solutions to the system.
Explanation:
In order to determine whether the two given points represent solutions to our system of equations, we must "plug" thos points into both equations and check that the equality remains valid.
Step 1: Plug
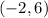 into
into
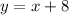

The solution verifies the equation.
Step 2: Plug
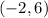 into
into

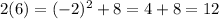
The solution verifies both equations. Therefore,
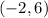 is a solution to this system.
is a solution to this system.
Now we must check if the second point is also valid.
Step 3: Plug
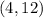 into
into
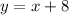

Step 4: Plug
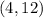 into
into

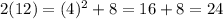
The solution verifies both equations. Therefore,
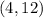 is another solution to this system.
is another solution to this system.