1 Answer

JanMensch · Answer 1 · 2020-10-10T01:03:58+0000

Hello!

The answer is:

The third option, the approximate magnitude of the given vector is 9.9 units.

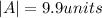
|A|=9.9units

To calculate the magnitude (length) of a vector, we need to apply the following formula:

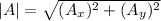
$|A|=\sqrt{(A_x)^(2) +(A_y)^(2) }$

So, we are given the vector:

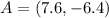
A=(7.6,-6.4)

Then, substituting and calculating the magnitude of the vector, we have:

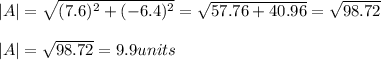
$|A|=\sqrt{(7.6)^(2) +(-6.4)^(2)}=√(57.76+40.96)=√(98.72)\\\\|A|=√(98.72)=9.9units$

Hence, we have that the correct option is the third option, the approximate magnitude of the given vector is 9.9 units.

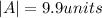
|A|=9.9units

Have a nice day!