Answer:
33 m/s
Step-by-step explanation:
By analyzing the vertical motion, we can find what is the time of flight of the projectile. The vertical position is
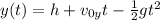
where
h = 20 m is the initial height
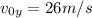 is the initial vertical velocity
is the initial vertical velocity
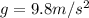 is the acceleration due to gravity
is the acceleration due to gravity
By putting y(t)=0, we find the time t at which the projectile hits the ground:
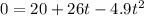
which has 2 solutions:
t = -0.7 s
t = 6.0 s
We discard the negative solution since it has no physical meaning. So, we know that the projectile hits the ground 6.0 s later after the launch.
The vertical velocity is given by
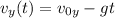
So we can find the vertical velocity when the projectile reaches point Q, by substituting t=6.0 s into this equation:
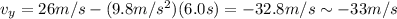
and the negative sign means the direction is downward.