Question

Two cars simultaneously left Points A and B and headed towards each other, and met after 2 hours and 45 minutes. The distance between points A and B is 264 miles. What is the speeds of the cars, if one of the cars travels 14 mph faster than the other?

Answer 1

55 miles per hour and 41 miles per hour.

Explanation:

Enjoy...It is correct because RSM told me so.

Answer 2

Hello!

The answer is:

`FirstCarSpeed=41mph\\SecondCarSpeed=55mph`

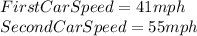
Why?

To calculate the speed of the cars, we need to write two equations in order to create a relation between the two speeds and be able to isolate one in function of the other.

So, let be the first car speed "x" and the second car speed "y", writing the equations we have:

For the first car:

`x_(FirstCar)=x_o+v*t`

For the second car:

We know that the speed of the second car is the speed of the first car plus 14 mph, so:

`x_(SecondCar)=x_o+(v+14mph)*t`

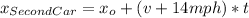
Now, we already know that both cars met after 2 hours and 45 minutes, meaning that positions will be the same at that moment, and the distance between A and B is 264 miles, so, we can calculate the relative speed between them:

If the cars are moving towards each other the relative speed will be:

`RelativeSpeed=FirstCarSpeed-(-SecondCarspeed)\\\\RelativeSpeed=x-(-x-14mph)=2x+14mph`

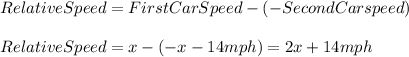
Then, since we know that they covered a combined distance which is equal to 264 miles of distance in 2 hours + 45 minutes, we have:

`2hours+45minutes=120minutes+45minutes=165minutes\\\\(165minutes*1hour)/(60minutes)=2.75hours`

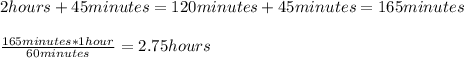
Writing the equation, we have:

`264miles=(2x+14mph)*t\\\\264miles=(2x+14mph)*2.75hours\\\\2x+14mph=(264miles)/(2.75hours)\\\\2x=96mph-14mph\\\\x=(82mph)/(2)=41mph`

We have that the speed of the first car is equal to 41 mph.

Now, for the second car we have that:

`SecondCarSpeed=FirstCarSpeed+14mph\\\\SecondCarSpeed=41mph+14mph=55mph`

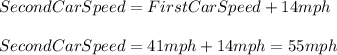
Hence, we have that:

`FirstCarSpeed=41mph\\SecondCarSpeed=55mph`

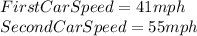
Have a nice day!