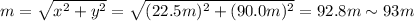Question

Can someone help me?!!!!!

Answer 1

93 m

Step-by-step explanation:

We need to find the resultant displacement.

Let's take north as positive y-direction and east as positive direction. We have

- Displacement 1 is 51 m to the north, so the two components are

`x_1 =0\\y_1 = 51 m`

- Displacement 2 is 45 m
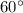`60^(\circ)` north of east, so the two components are

`x_1 = (45)cos 60^(\circ)=22.5 m\\y_1 = (45) sin 60^(\circ)=39.0 m`

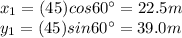
So to find the resultant displacement we have to sum the components along each direction:

`x=x_1 + x_2 = 0+22.5 m = 22.5 m\\y = y_1 + y_2 = 51 m +39.0 m = 90.0 m`

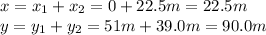
And the magnitude of the resultant displacement is

`m=√(x^2+y^2)=√((22.5 m)^2+(90.0 m)^2)=92.8 m \sim 93 m`