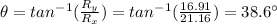Question

PLEASE HELP!

Find the angle of the resultant vector for the vectors shown below. (nearest whole number and angles measured from the positive x-axis)
vector

A) 39 degrees


B) 51 degrees



C) 70 degrees

Answer 1

`38.6^(\circ)`

Step-by-step explanation:

In order to find the resultant of the two vectors, we need to find the components of each vector along the x- and y- axis.

For the horizontal vector, we have:

x-component:
`A_x = 15`

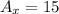
y-component:
`A_y = 0`

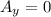
For the vectors of 18 units:

x-component:
`B_x = 18 cos 70^(\circ)=6.16`

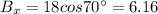
y-component:
`B_y = 18 sin 70^(\circ)=16.91`

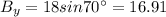
So the components of the resultant vector are

`R_x=A_x + B_x = 15 +6.16 = 21.16`

`R_y=A_y + B_y = 0 +16.91 = 16.91`

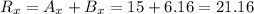
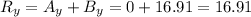
And so the direction is given by

`\theta = tan^(-1) ((R_y)/(R_x))=tan^(-1) ((16.91)/(21.16))=38.6^(\circ)`