Question

The current flowing through an electric circuit is the derivative of the charge as a function of time. If the charge q is given by the equation q(t)=3t^2+2t-5 what is the current at t = 0?

Answer 1

Answer: I just took the test and got 100%

1. C, 2

2. D, v(t) = 8t - 2

3. B, 902 mi/min

4. A, the car is slowing down at a rate 10 mi/h^2

Answer 2

The current at t = 0 is

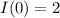`I (0) = 2` units of current

Explanation:

If the current flowing through an electric circuit is defined as the derivative of the charge as a function of time and we have the equation of the charge as a function of time, then, to find the equation of the current, we derive the equation of the charge.

`q (t) = 3t ^ 2 + 2t-5`

`(dq(t))/(dt) = 3 (2) t ^ {2-1} +2t ^ {1-1} -0`

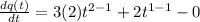
Simplifying the expression we have:

`(dq(t))/(dt) = 6t + 2t ^0\\\\(dq(t))/(dt) = 6t + 2 = I (t)`

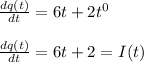
Finally, the equation that defines the current of this circuit as a function of time is:

`I (t) = 6t +2`

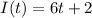
Now to find the current at t = 0 we make
`I (t = 0)`

`I (0) = 6 * 0 +2`

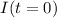
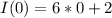
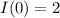`I (0) = 2` units of current