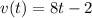Question

The equation for the position of an object at time t is represented by the equation f(t)=4t^2-2t. Which equation represents the instantaneous velocity at any given time, t?

Answer 1

Answer: I just took the test and got 100%

1. C, 2

2. D, v(t) = 8t - 2

3. B, 902 mi/min

4. A, the car is slowing down at a rate 10 mi/h^2

Answer 2

The equation that represents the instantaneous velocity at any given time, t is:

`v (t) = 8t -2`

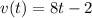
Explanation:

In physics, the equation that describes the instantaneous velocity of an object is the derivative of the position of this object as a function of time.

In this problem we have the function that describes the position of the object at a time t.

`f (t) = 4t ^ 2-2t`

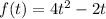
Therefore to obtain the instantaneous velocity we derive f (t) with respect to time

`(df(t))/(dt) = 2(4)t-2\\\\(df(t))/(dt) = 8t-2 = v (t)`

Finally the equation of velocity is:

`v (t) = 8t -2`