Question

A 4-digit number ends in 3. If you put the number 3 in the first position, the number will decrease by 738. Find the original 4-digit number.

Answer 1

4153

Explanation:

Answer 2

4153

Explanation:

Let the original number be
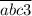`\overline{abc3}` [a is the number of thousands, b - the number of hundreds, c - the number of tens, 3 - the number of ones]

If you put the number 3 in the first position, the number will be
`\overline{3abc}`

New number is 738 less than old number.

When you subtract from 3 some number c and get 8, then you have to lend one ten and subtract this number c from 13. So, 13-5=8. Thus, c=5. Remember about lending! Now when you subtrat from 4 (not 5 because of lending) some number b and get 3, then b=1. Now when you subtract from 1 some number a and get 7, then you have to lend 1 from the number of thousands and subtract a from 11 to get 7, thus 11-4=7 and a=4.

We get initial number 4153 and rewritten number 3415. Check the difference:

4153-3415=738