Question

Two cyclists left simultaneously from cities A and B heading towards each other at constant rates and met in 5 hours. The rate of the cyclist from A was 3 mph less than the rate of the other cyclist. If the cyclist from B had started moving 30 minutes later than the other cyclist, then the two cyclists would have met 31.8 miles away from A. What is the distance between A and B, in miles?

Answer 1

73.92 miles

Explanation:

Formula for calculating distance = speed × time

Rate/speed of cyclist from city A = ( x - 3 ) mph , Time Taken = 5 Hours

Rate/speed of cyclist from city B = x mph

If Cyclist from B had started moving 30 minutes later

Time Taken by cyclist from B = 4.5 Hours

If B had started 30 minutes later, then the two cyclist would have met 31.8 miles from A.

distance covered by cyclist from A = 31.8

Solution:

For city A:

distance = speed × time

31.8 = ( x - 3 ) × 5 ⇒
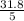`(31.8)/(5)` = x - 3

6.36 = x - 3 ⇒ x = 6.36 + 3 ⇒ x = 9.36 mph

For city B:

distance = speed × time

= 9.36 × 4.5

= 42.12 miles

Distance between A and B = 31.8 + 42.12

= 73.92 miles