Question

a ball is thrown with a slingshot at a velocity of 110ft/sec at an angle of 20 degrees above the ground from a height of 4.5 ft. approximentaly how long does is take for the ball to hit the ground. Acceleration due to gravity is 32ft/s^2

Answer 1

`t=2.47\ s`

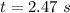
Explanation:

The equation that models the height of the ball in feet as a function of time is

`h(t) = h_0 + s_0t -16t ^ 2`

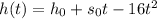
Where
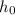`h_0` is the initial height,
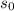`s_0` is the initial velocity and t is the time in seconds.

We know that the initial height is:

`h_0 = 4.5\ ft`

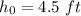
The initial speed is:

`s_0 = 110sin(20\°)\\\\s_0 = 37.62\ ft/s`

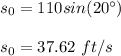
So the equation is:

`h (t) = 4.5 + 37.62t -16t ^ 2`

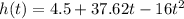
The ball hits the ground when when
`h(t) = 0`

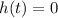
So

`4.5 + 37.62t -16t ^ 2 = 0`

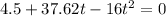
We use the quadratic formula to solve the equation for t

For a quadratic equation of the form

`at^2 +bt + c`

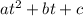
The quadratic formula is:

`t=(-b\±√(b^2 -4ac))/(2a)`

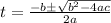
In this case

`a= -16\\\\b=37.62\\\\c=4.5`

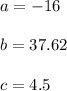
Therefore

`t=(-37.62\±√((37.62)^2 -4(-16)(4.5)))/(2(-16))`

`t_1=-0.114\ s\\\\t_2=2.47\ s`

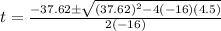
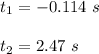
We take the positive solution.

Finally the ball takes 2.47 seconds to touch the ground