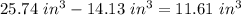Question

A sports company wants to package a ball with a 1.5-inch radius in sets of two. They have two options: a cylinder or a square prism.

The company wants to use the package that has the least amount of wasted space. The company should choose

a.)the prism because it has approximately 11.6 in.3 less wasted space than the cylinder.
b.)the prism because it has approximately 14.1 in.3 less wasted space than the cylinder.
c.)the cylinder because it has approximately 11.6 in.3 less wasted space than the prism.
d.)the cylinder because it has approximately 14.1 in.3 less wasted space than the prism.

Answer 1

C. the cylinder because it has approximately 11.6 in.3 less wasted space than the prism.

Explanation:

if you find the volumes of both shapes and subtract the volumes of the two balls and then subtract the two remaining values you get a difference of 11.6 inches. This makes the cylinder smaller and therefore uses less space.

Answer 2

Option c.) the cylinder because it has approximately 11.6 in.3 less wasted space than the prism.

Explanation:

step 1

Find the volume of one ball

The volume of the sphere is equal to

`V=(4)/(3)\pi r^(3)`

we have

`r=1.5\ in`

`V=(4)/(3)(3.14)(1.5)^(3)=14.13\ in^(3)`

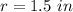
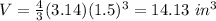
therefore

The volume of two balls is

`(2)*14.13=28.26\ in^(3)`

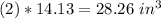
step 2

Find the volume of the cylinder

The volume of the cylinder is equal to

`V=\pi r^(2)h`

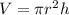
we have

`r=1.5\ in`

`h=1.5*4=6\ in`

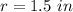
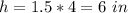
substitute

`V=(3.14)(1.5)^(2)(6)=42.39\ in^(3)`

therefore

The wasted space with the cylinder is equal to

`42.39\ in^(3)-28.26\ in^(3)=14.13\ in^(3)`

step 3

Find the volume of the square prism

The volume of the square prism is equal to

`V=b^(2)h`

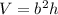
we have

`b=1.5*2=3\ in`

`h=1.5*4=6\ in`

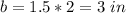
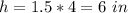
substitute

`V=(3)^(2)(6)=54\ in^(3)`

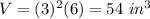
therefore

The wasted space with the prism is equal to

`54\ in^(3)-28.26\ in^(3)=25.74\ in^(3)`

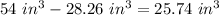
step 4

Find the difference of the wasted space

`25.74\ in^(3)-14.13\ in^(3)=11.61\ in^(3)`