Question

The given line segment has a midpoint at (3, 1).

What is the equation, in slope-intercept form, of the perpendicular bisector of the given line segment?

y = x
y = x – 2
y = 3x
y = 3x − 8

Answer 1

Answer: The answer is y= x/3

Step-by-step explanation:

Given points =(2,4) and (4,-2) whose mid point is (3,1)

Let the points be named as A(2,4) and B(4,-2) and mid point as C(3,1)

So slope of AB =
`(4-(-2))/(2-4)`

=
`(6)/(-2)`

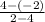
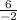
= -3

We know that Product of Slope of perpendicular lines = -1

Now slope of the line perpendicular to AB × slope of AB = -1

-3 × m2 =-1

i.e. m2 =
`(1)/(3)`

Now equation of perpendicular bisector of AB passing through C(3,1) is

`y -1 =(1)/(3)(x-3)\\`

`y= 1+(1)/(3)x -1`

`y=(1)/(3)x`

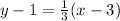
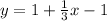
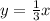
Hence the equation of line is y =x/3

Answer 2

y = 1/3 x.

Explanation:

The slope of the given line is

(4 - (-2) / 2 - 4)

= -3.

So the slope of the line perpendicular to it = -1 / (-3) = 1/3.

This line also passes through the point (3, 1) so its equation is ( by the point-slope form):

y - 1 = 1/3(x - 3)

y - 1 = 1/3x - 1

y = 1/3 x (answer).