Question

The value in dollars, v(x), of certain truck after x year’s is represented by the equation v(x)= 32500(0.92)^x. To the nearest dollar, how much is the truck worth after 2 years?

Answer 1

`\bf v(x)=32500(0.92)^x\qquad \qquad \stackrel{\textit{2 years later, x = 2}}{v(2)=32500(0.92)^2} \\\\\\ v(2)=32500(0.8464)\implies v(2)=27508`

Answer 2

$27508.

Explanation:

We have been given that the value of certain truck after x years is represented by equation
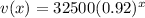`v(x)=32500(0.92)^x`. We are asked to find the value of truck after 2 years.

To find truck's value after 2 years, we need to substitute
`x=2` in our given equation.

`v(2)=32500(0.92)^2`

`v(2)=32500*0.8464`

`v(2)=27508`

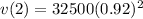
Therefore, the truck is worth $27508 after 2 years.