Question

Given: AB ≅ BC BD − median of ΔABC, m∠ABD = 40° Find: m∠ABC, m∠BDC

Answer 1

m∠ABC= 80°, m∠BDC= 90°

Explanation:

If m∠ABD = 40°, then add 40°+40° to get m∠ABC because AB ≅ BC, meaning their angles would be congruent.

For m∠BDC, just look at the picture and deduce that it's a 90 degree angle.

Answer 2

m∠ABC=80° and m∠BDC=90°

Explanation:

Given the ΔABC in which AB ≅ BC, m∠ABD = 40° and BD is median of ΔABC.

we have to find the measure of angle ∠ABC and ∠BDC.

As the median of isosceles triangle split the angle at the vertex into two equal parts i.e ∠ABC is twice the angle ∠ABD

⇒
`\angle ABC=2\angle ABD`

`\angle ABC=2* 40=80^(\circ)`

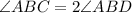
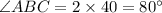
Also the median of isosceles triangle is perpendicular to the opposite side i.e to the base. Here, BD is perpendicular to AC

⇒ ∠BDC=90°

Therefore, the measure of angle ABC and BDC is 80° and 90° respectively.