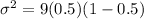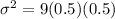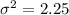Question

Problem: A fair coin is flipped nine times and the numbers of heads are counted. Question: What is the variance for this distribution?

5 points
2.25
0.5
4.5
9

Answer 1

Answer: Option A

`\sigma ^ 2 = 2.25`

Explanation:

The number of faces obtained by flipping the coin 9 times is a discrete random variable.

If we call this variable x, then, the probability of obtaining a face in each test is p.

Where
`p = 0.5`

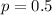
If we call n the number of trials then:

`n = 9`

The distribution of this variable is binomial with parameters

`p = 0.5\\\\n = 9`

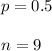
For a binomial distribution, the variance "
`\sigma^2`" is defined as

`\sigma ^ 2 = np(1-p)`

`\sigma ^ 2 = 9(0.5)(1-0.5)`

`\sigma ^ 2 = 9(0.5)(0.5)`

`\sigma ^ 2 = 2.25`