Question

The ratio of the volumes of the similar solids is _____ 25:1 5:1 125:1

The ratio of the surface areas of the similar solids is _____ 125:1 5:1 25:1
The ratio of the heights of the similar solids_____ 125:1 5:1 25:1
Two spheres with different radii measurements are_____ similar (always, never sometimes)
The length of the diameter of a sphere is 8 inches. The volume of the sphere is____ the surface area of the sphere. (less than, greater than, equal to)

Answer 1

Part 1)

a) The ratio of the heights of the similar solids is 5/1

b) The ratio of the surface areas of the similar solids is (5/1)²=25/1

c) The ratio of the volumes of the similar solids is (5/1)³=125/1

Part 2) Two spheres with different radii measurements are always similar

Part 3) The volume of the sphere is greater than the surface area of the sphere

Explanation:

Part 1) we know that

The ratio of the corresponding heights of the similar solids is equal to the scale factor

The ratio of the surface areas of the similar solids is equal to the scale factor squared

The ratio of the volumes of the similar solids is equal to the scale factor elevated to the cube

In this problem

The scale factor is 5/1

therefore

a) The ratio of the heights of the similar solids is 5/1

b) The ratio of the surface areas of the similar solids is (5/1)²=25/1

c) The ratio of the volumes of the similar solids is (5/1)³=125/1

Part 2)

we know that

Figures can be proven similar if one, or more, similarity transformations (reflections, translations, rotations, dilations) can be found that map one figure onto another.

In this problem to prove that two spheres are similar, a translation and a scale factor (from a dilation) will be found to map one sphere onto another.

therefore

Two spheres with different radii measurements are always similar

Part 3) The length of the diameter of a sphere is 8 inches

The volume of the sphere is equal to

`V=(4)/(3)\pi r^(3)`

we have

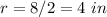`r=8/2=4\ in` -----> the radius is half the diameter

substitute

`V=(4)/(3)\pi (4)^(3)`

`V=85.33\pi\ in^(3)`

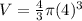
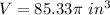
The surface area of the sphere is equal to

`SA=4\pi r^(2)`

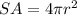
substitute

`SA=4\pi (4)^(2)`

`SA=64\pi\ in^(2)`

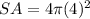
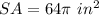
therefore

The volume of the sphere is greater than the surface area of the sphere