Answer:
4th Graph is correct option.
Explanation:
Given Function is ,
f(x) = ( x - 1 )( x + 4 )
f(x) = x² + 3x - 4
Since, we are given a quadratic function.
So, Graph is a parabola.
Now we find the vertex of the parabola by expressing given function in standard form of parabola.
Consider,
y = x² + 3x - 4
x² + 3x = y + 4
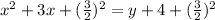
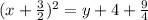
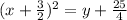
By comparing this equation with ( x - h )² = 4a( y - k )
where, ( h , k ) is vertex of the parabola.
⇒ Vertex of the given function =
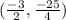
These coordinates of the vertex lie in 3rd Quadrant.
Now looking at all given graphs. Only 4th Graph has vertex in 3rd quadrant.
Therefore, 4th Graph is correct option.