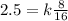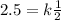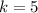Answer:
The constant of variation is
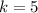
Explanation:
First we must write the relationship as an equality.
If q varies inversely with the square of m, this means that when m ^ 2 increases then q decreases.
If q varies directly with the product of r and x this means that when r * x increases q increases.
Then the relationship is:
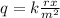
Where k is the constant of proportionality
Then if:
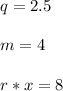
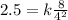
We solve for k