Question

What is the smallest value of an angle, , by which a regular pentagon should be rotated about its center x so that it carries onto itself?

Answer 1

`x = 72^(\circ)`

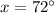
Step-by-step explanation:

Given

Shape: Regular Pentagon

Required

Determine the minimum value of x

A pentagon has 5 sides and 1 complete rotation of a pentagon about its centre is 360 degrees

i.e.

`1\ Rotation = 360^(\circ)`

`Sides= 5`

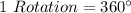
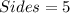
The angle of rotation (x) is then calculated as:

`x = (1\ Rotation)/(Sides)`

Substitute values for 1 rotation and sides

`x = (360^(\circ))/(5)`

`x = 72^(\circ)`

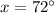
The above is the minimum value of rotation.

As a bonus

Other possible angle of rotation must be in multiples of 72

i.e.

`x = 72, 144, 216, 288,360....`

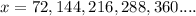
This means that when the pentagon is rotated in any of the above angles of rotation, it will be carried onto itself.