Question 14 Math Help please

Question

asked Mar 12, 2020 194k views

1 Answer

William Edmisten · Answer 1 · 2020-03-18T22:08:28+0000

ANSWER

(1,0) is a solution

Step-by-step explanation

The given inequality is

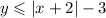
$y \leqslant |x + 2|- 3$

We substitute the point to see which ones satisfy the inequality.

For (1,0)

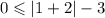
$0\leqslant|1+ 2|- 3$

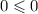
$0\leqslant 0$

This is true.

(1,0) is a solution.

For (-1-1)

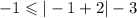
$- 1\leqslant | - 1 + 2|-3$

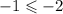
$- 1\leqslant-2$

False

(-1,-1) is not a solution.

For (0,0)

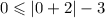
$0\leqslant|0+2|-3$

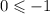
$0\leqslant- 1$

False.

For (0,1)

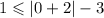
$1\leqslant|0+ 2|-3$

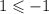
$1\leqslant-1$

This is also false