Part A
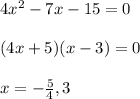
So, the x-intercepts are
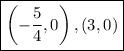
Part B
The vertex will be a minimum because the coefficient of
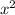 is positive.
is positive.
The x-coordinate of the vertex is
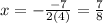
Substituting this back into the function, we get
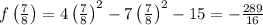
So, the coordinates of the vertex are
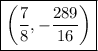
Part C
Plot the vertex and the x-intercepts and draw a parabola that passes through these three points.
The graph is shown in the attached image.