Question

HELP!

(08.07 HC)
An expression is shown below:
f(x) = 4x² - 7x - 15
Part A: What are the x-intercepts of the graph of f(x)? Show your work. (2 points)
Part B: Is the vertex of the graph of f(x) going to be a maximum or minimum? What are the
coordinates of the vertex? Justify your answers and show your work. (3 points)
Part C: What are the steps you would use to graph f(x)? Justify that you can use the answers
obtained in Part A and Part B to draw the graph. (5 points)
(10 points)

Answer 1

Part A

`4x^2 -7x-15=0\\\\(4x+5)(x-3)=0\\\\x=-(5)/(4), 3`

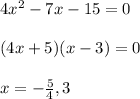
So, the x-intercepts are
`\boxed{\left(-(5)/(4), 0 \right), (3,0)}`

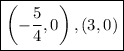
Part B

The vertex will be a minimum because the coefficient of
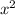`x^2` is positive.

The x-coordinate of the vertex is
`x=-(-7)/(2(4))=(7)/(8)`

Substituting this back into the function, we get
`f\left((7)/(8) \right)=4\left((7)/(8) \right)^2 -7\left((7)/(8) \right)^2 -15=-(289)/(16)`

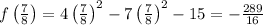
So, the coordinates of the vertex are
`\boxed{\left((7)/(8), -(289)/(16) \right)}`

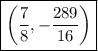
Part C

Plot the vertex and the x-intercepts and draw a parabola that passes through these three points.

The graph is shown in the attached image.