Question

Kari wants to measure the height of a tree. She walks exactly 105 feet away from the base of the tree and looks up to the top of it. The angle from the ground to the top of the tree is 33 degrees. This particular tree grows at an angle of 86 degrees with respect to the ground rather than vertically. How tall is the tree to the nearest tenth of a foot?

Answer 1

68.2 feet

Explanation:

The angle of elevation, the one from the ground up, is given as 33 degrees. If Kari is 105 feet from the tree, that serves as the measure of the base of the right triangle. We are looking for the height of the tree, which is the side opposite the angle. What we have, then, is the angle (33 degrees), the side adjacent to the angle (105 ft), and we are looking for the side opposite the angle (x). What we need to use is the tangent ratio, which relates the side opposite the angle to the side adjacent to the angle, as follows:

`tan33=(x)/(105)`

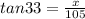
To solve for x we multiply both sides of the equation by 105 to get 105tan33°=x. Plug that into your calculator in degree mode to get 68.18779729. Round from there to get 68.2 feet.