Question

Write an equation for a cosine function with an amplitude of 3, a period of 2, a phase shift of -2, and a vertical displacement of 5.

y=3cos⁡2π(x+2)+5


y=3cos⁡2π(x−5)+2


y=5cos⁡3π(x−2)+2


y=3cos⁡2π(x+2) / 2+5

Answer 1

Last option

`y = 3cos(\pi(x+2)) + 5`

Explanation:

The general cosine function has the following form

`y = Acos(b(x-\phi)) + k`

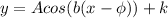
Where A is the amplitude: half the vertical distance between the highest peak and the lowest peak of the wave.

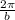`(2\pi)/(b)` is the period: time it takes the wave to complete a cycle.

k is the vertical displacement.

`\phi` is the shift phase

In this problem :

`A = 3`

`(2\pi)/(b)=2\\\\ b=(2\pi)/(2)\\\\ b=\pi`

`\phi =-2\\\\k = 5`

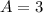
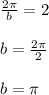
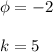
So The function is:

`y = 3cos(\pi(x+2)) + 5`