Answer:
1) "The plans will pay the same at 8 correct questions"
2) "The amount they'll pay at that number of questions is $1600"
3) "You think you can answer 9 questions correctly. Which plan should you choose? Plan B."
Explanation:
We can represent each of the two prize plans with a linear equation. Let
be the number of questions a player gets right and let
be the total money earned through the final round.
Plan A:
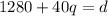
Plan B:
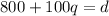
1) Since these are linear equations (ie. lines), we can find the intersection in two ways.
(1) Plot a graph
(2) Set equations equal to each other.
I will show (2) but you can confirm by plotting these two lines on a graph.
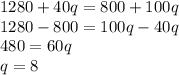
This means that if you get 8 questions correct, both prize plans will return the same amount of money. Therefore the first question is...
"The plans will pay the same at 8 correct questions"
2) To answer the second statement we simply plug in 8 into either equation. Remember at 8 questions, both prizes give you the same amount of money, so it doesn't matter which equation we select. I will plug 8 into Plan B.
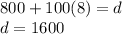
So the second question's answer is...
"The amount they'll pay at that number of questions is $1600"
3) To answer the third and final question. We can simply plug in 9 into each equation and compare. However, a shortcut is to notice that Plan B will give more money for each correct answer. And since 9 questions is greater than our point of intersection 8, Plan B will result in more money.
"You think you can answer 9 questions correctly. Which plan should you choose? Plan B"