Answer:
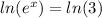
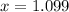
Explanation:
You have the following exponential expression:
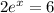
You need to divide both sides of the equation by 2:
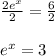
Now apply the function Natural logarithm to both sides of the function:
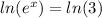
Note that now the exponential function is transformed into a logarithmic function.
By definition:
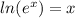 Because the base of the Natural logarithm is the Euler's number "e".
Because the base of the Natural logarithm is the Euler's number "e".
Then you can solve for "x":
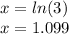 )
)