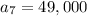Question

A house worth $70,000 when purchased was worth $67,000 after the first year and $64,000 after the second year. If the economy does not improve and this trend continues, what will be the value of the house after 7 years? a) Write an explicit formula for the sequence. Explain where you found the numbers you are putting in the formula. b) Identify the value of n and explain where you found it. Use the explicit formula to solve the problem.

Answer 1

a) The formula for the sequence is

`a_n = 67,000 -3,000(n-1)`

b)
`a_7 = 49,000`

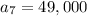
Explanation:

Note that the difference between any two consecutive terms in the sequence is always equal to $3,000

`67,000-70,000= -3,000\\\\64,000-67,000=-3,000`

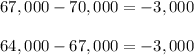
Then we have an arithmetic sequence where each term increases by a magnitude of 3,000 with respect to the previous term.

The explicit formula for an arithmetic sequence is:

`a_n = a_1 +d(n-1)`

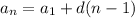
Where d is the common difference between the consecutive terms of the sequence

`d = -3,000`

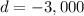
`a_1` is the first term, or the value of the house after year 1
`a_1= 67,000`

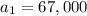
n represents the number of years since the house was purchased

With

n={0, 1, 2, 3, 4, 5, 6, 7,.., n}

a) Then the formula for the sequence is

`a_n = 67,000 -3,000(n-1)`

With

n={0, 1, 2, 3, 4, 5, 6, 7,.., n}

---------------------------------------------------------------------------------------------

b) Now we can use the formula to find the price of the house after 7 years

`a_7 = 67,000 -3,000(7-1)`

`a_7 = 67,000 -3,000(6)`

`a_7 = 49,000`