Question

Determine whether the relationship between the circumference of a circle and its diameter is a direct variation. If so, identify the constant of proportionality. Justify your response.

Answer 1

The relationship between the circumference of a circle and its diameter represent a direct variation

The constant of proportionality is equal to
`\pi`

Explanation:

we know that

A relationship between two variables, x, and y, represent a direct variation if it can be expressed in the form
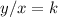`y/x=k` or
`y=kx`

The circumference of a circle is equal to

`C=\pi D`

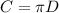
Let

C=y

D=x

substitute

`y=\pi x`

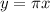
therefore

The relationship between the circumference of a circle and its diameter represent a direct variation

The constant of proportionality is equal to
`\pi`