Question

A bicycle manufacturer uses the given expression to model the monthly profit from sales of a new model of bicycle, where x is the selling price of one bicycle, in dollars. At what selling prices for the bicycle will the manufacturer make neither a profit nor a loss?

Answer 1

The manufacturer will have no profit or loss when the selling price equals $200 or $100.

Explanation:

The expression to model the monthly profit from sales of a new model of bicycle is

-x^2 + 300x -20,000

Let

f(x) -----> the monthly profit in dollars

x -----> s the selling price of one bicycle in dollars

`f(x)= -x^(2)+300x-20,000`

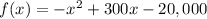
we know that

The manufacturer will make no profit nor a loss when the profit is equal to zero

so

f(x)=0

`-x^(2)+300x-20,000=0`

Multiply by -1 both sides

`x^(2)-300x+20,000=0`

The formula to solve a quadratic equation of the form
`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`a=1\\b=-300\\c=20,000`

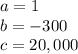
substitute in the formula

`x=\frac{300(+/-)\sqrt{-300^(2)-4(1)(20,000)}}{2(1)}`

`x=(300(+/-)√(10,000))/(2)`

`x=(300(+/-)100)/(2)`

`x=(300(+)100)/(2)=200`

`x=(300(-)100)/(2)=100`

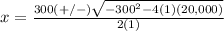
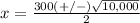
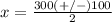
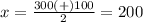
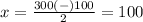
therefore

The manufacturer will have no profit or loss when the selling price equals $200 or $100.