Question

If the determinant of this matrix is -19, what is the value of a?

A.
3
B.
4
C.
5
D.
6

Answer 1

a = 5

Explanation:

We are given 3 x 3 matrix and the determinant of the matrix is -19.

We need find the value of "a" in the given matrix.

`\left[\begin{array}{ccc}-6&7&1\\a&-3&4\\-6&4&-3\end{array}\right]`

determinant (D) = -6[(-3)(-3) − (4)(4)] − 7[a(-3) − (4)(-6)] + 1[a(4) − (-3)(-6)]

-19 = -6[9 - 16] -7[-3a +24] +1[4a - 18]

-19 = -6[-7] +21a - 168 + 4a - 18

-19 = 42 + 21a -168 + 4a - 18

Simplify the like terms, we get

-19 = 25a - 144

25a = -144 + 19

25a = 125

Dividing both sides by 25, we get

a =
`(125)/(25)`

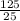
a = 5

So the value of a is 5.

Answer 2

C)5

Explanation:

For a 3x3 matrix
`\left[\begin{array}{ccc}a&b&c\\d&e&f\\g&h&i\end{array}\right]`

determinent is given by = = a(ei − fh) − b(di − fg) + c(dh − eg)

Given Matrix

`\left[\begin{array}{ccc}-6&7&1\\a&-3&4\\-6&4&-3\end{array}\right]`

determinent of matrix= -6((-3)(-3) − (4)(4)) − 7(a(-3) − (4)(-6)) + 1(a(4) − (-3)(-6))

-19= -6(9-16) - 7(-3a+24) +4a-18

125= 25a

125/25= 25a/25

a= 5 !