Explanation:
Because the length of ST is calculated using pythagorean theorem:
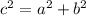
Where the square of the hypotenuse is equal to the sum of squares of the other two sides of a right triangle. In this case, the hypotenuse is ST and the other two sides are distances between S and T over the X and Y axis. Those are easily calculated:
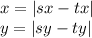
Where x is the distance between S and T over X axis and Y distance over Y axis, sx and tx are X coordinates of S and T, sy and ty are Y coordinates of S and T.
Using that formula, you get that y = 17 and x = 8.
Back to the pythagorean theorem, if we put those number in the formula of the pythagorean theorem, we get something like this:
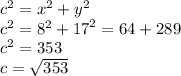
And finally, the correct answer is in fact 353.