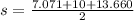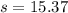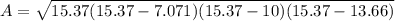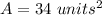Question

Find the area of the given triangle to the nearest square unit. Angle a= 30 degrees, b=10, angle B=45 degrees

Answer 1

`A=34\ units^2`

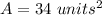
Explanation:

Suppose we have a general triangle like the one shown in the figure.

We know the angle A, the angle B and the length b.

`A = 30\°\\\\B = 45\°\\\\b = 10`

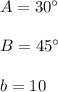
By definition I know that the sum of the internal angles of a triangle is always equal to 180 °.

So

`A + B + C = 180\\\\30 + 45 + C = 180`

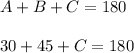
We solve the equation and thus we find the angle C.

`C = 180 - 30-45\\\\C = 105`

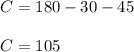
We already know the three triangle angles.

Now we use the sine theorem to calculate the sides c and a.

The sine theorem says that:

`(sin(A))/(a)=(sin(B))/(b)=(sin(C))/(c)`

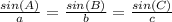
Then

`(sin(30))/(a)=(sin(45))/(10)`

`(sin(30))/((sin(45))/(10))=a`

`a=7.071`

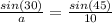
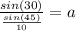
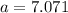
Also

`(sin(105))/(c)=(sin(45))/(10)`

`(sin(105))/((sin(45))/(10))=c`

`c=13.660`

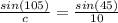
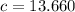
Finally, we use the Heron formula to calculate the triangle area

`A=√(s(s-a)(s-b)(s-c))`

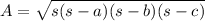
Where s is:

`s=(a+b+c)/(2)`

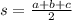
Therefore

`s=(7.071+10+13.660)/(2)`

`s=15.37`

`A=√(15.37(15.37-7.071)(15.37-10)(15.37-13.66))`

`A=34\ units^2`