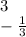Question 1:
For this case we have that by definition, if a and b are two parallel lines, then the corresponding angles are congruent, that is, we can write 3x + 2 and x + 8 as supplementary angles:
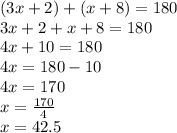
We look for the value of the angles:
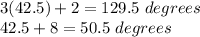
ANswer:
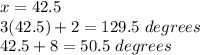
Question 2:
For this case we have that by definition, the equation of a line of the slope-intersection form is given by:

Where:
m: It's the slope
b: It is the cutoff point with the y axis
Now, in the equation
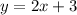
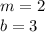
By definition, if two lines are parallel, their slopes are equal. Also, if two lines are perpendicular, then the product of their slopes is -1.
So:
The slope of a line parallel to the given line is:

The slope of a line perpendicular to the given line is:

ANswer: