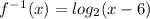Answer:
The answer is D
Explanation:
In order to find out the inverse of the function, you have to express a new function where the independent variable must be "y" instead of "x".
So, you have to reorganize the base function and then free the variable "x".
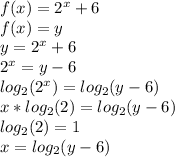
Then, we recall "y" as "x" and
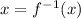
Finally, the answer is: