11. Find discriminant.
Answer: D) 0, one real solution
A quadratic function is given of the form:
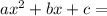
We can find the roots of this equation using the quadratic formula:
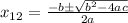
Where
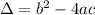 is named the discriminant. This gives us information about the roots without computing them. So, arranging our equation we have:
is named the discriminant. This gives us information about the roots without computing them. So, arranging our equation we have:

Since the discriminant equals zero, then we just have one real solution.
12. Find discriminant.
Answer: D) -220, no real solution
In this exercise, we have the following equation:
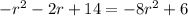
So we need to arrange this equation in the form:
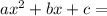
Thus:

So the discriminant is:
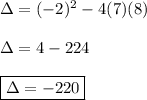
Since the discriminant is less than one, then there is no any real solution
13. Value that completes the squares
Answer: C) 144
What we need to find is the value of
 such that:
such that:

is a perfect square trinomial, that are given of the form:
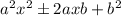
and can be expressed in squared-binomial form as:
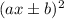
So we can write our quadratic equation as follows:
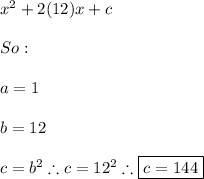
Finally, the value of
 that completes the square is 144 because:
that completes the square is 144 because:

14. Value that completes the square.
Answer: C)
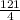
What we need to find is the value of
 such that:
such that:
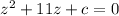
So we can write our quadratic equation as follows:
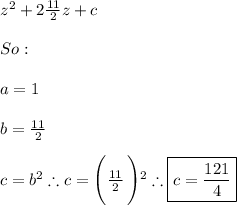
Finally, the value of
 that completes the square is
that completes the square is
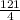 because:
because:

15. Rectangle.
In this problem, we need to find the length and width of a rectangle. We are given the area of the rectangle, which is 45 square inches. We know that the formula of the area of a rectangle is:
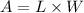
From the statement we know that the length of the rectangle is is one inch less than twice the width, this can be written as:

So we can introduce this into the equation of the area, hence:

The only valid option is
 because is greater than zero. Recall that we can't have a negative value of the width. For the length we have:
because is greater than zero. Recall that we can't have a negative value of the width. For the length we have:

Finally:
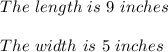
16. Satellite
The distance in miles between mars and a satellite is given by the equation:

where
 is the number of hours it has fallen. So we need to find when the satellite will be 452 miles away from mars, that is,
is the number of hours it has fallen. So we need to find when the satellite will be 452 miles away from mars, that is,
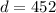 :
:
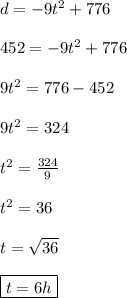
Finally, the satellite will be 452 miles away from mars in 6 hours.