Question

Find all polar coordinates of point P where P = ordered pair 4 comma negative pi divided by 3.

Answer 1

`(4,-(\pi)/(3)+2n\pi)` And
`(-4,-(\pi)/(3)+(2n+1)\pi).`

Hope this helps you out!

Answer 2

All the polar coordinates of point P are
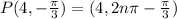`P(4,-(\pi)/(3))=(4,2n\pi-(\pi)/(3))` and
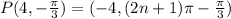`P(4,-(\pi)/(3))=(-4,(2n+1)\pi-(\pi)/(3))`, where n is any integer and θ is in radian.

Explanation:

It a polar coordinate is given as P(r,θ), then all the polar coordinates of point P are defined as

`P(r,\theta)=(r,2n\pi+\theta)`

`P(r,\theta)=(-r,(2n+1)\pi+\theta)`

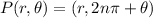
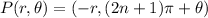
Where, n is any integer and θ is in radian.

The given point is

`P(4,-(\pi)/(3))`

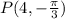
So, all the polar coordinates of point P are defined as

`P(4,-(\pi)/(3))=(4,2n\pi-(\pi)/(3))`

`P(4,-(\pi)/(3))=(-4,(2n+1)\pi-(\pi)/(3))`

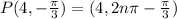
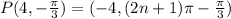
Therefore all the polar coordinates of point P are
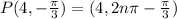`P(4,-(\pi)/(3))=(4,2n\pi-(\pi)/(3))` and
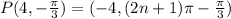`P(4,-(\pi)/(3))=(-4,(2n+1)\pi-(\pi)/(3))`, where n is any integer and θ is in radian.