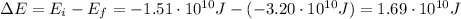Question

A 525 kg satellite is in a circular orbit at an altitude of 575 km above the Earth's surface. Because of air friction, the satellite eventually falls to the Earth's surface, where it hits the ground with a speed of 1.90 km/s. How much energy was transformed into internal energy by means of air friction? 14457750000 Incorrect: Your answer is incorrect.%20orbit%20at%20an%20altitude%20of%20575%20km%20above%20the%20Earth's%20surface.%20Because%20of%20air%20friction%2C%20the%20satellite%20eventually%20falls%20to%20the%20Earth's%20surface%2C%20where%20it%20hits%20the%20ground%20with%20a%20speed%20of%201.90%20km%2Fs.%20How%20much%20energy%20was%20transformed%20into%20internal%20energy%20by%20means%20of%20air%20friction%3F%20%20%20%20J/study?trackid=ae7684c4b7d0&strackid=e93f14d66685&event=enter_submit#p=1

Answer 1

`1.69\cdot 10^(10)J`

Step-by-step explanation:

The total energy of the satellite when it is still in orbit is given by the formula

`E=-G(mM)/(2r)`

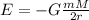
where

G is the gravitational constant

m = 525 kg is the mass of the satellite

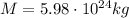`M=5.98\cdot 10^(24)kg` is the Earth's mass

r is the distance of the satellite from the Earth's center, so it is the sum of the Earth's radius and the altitude of the satellite:

`r=R+h=6370 km +575 km=6945 km=6.95\cdot 10^6 m`

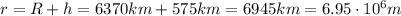
So the initial total energy is

`E_i=-(6.67\cdot 10^(-11))((525 kg)(5.98\cdot 10^(24) kg))/(2(6.95\cdot 10^6 m))=-1.51\cdot 10^(10)J`

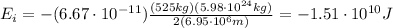
When the satellite hits the ground, it is now on Earth's surface, so

`r=R=6370 km=6.37\cdot 10^6 m`

so its gravitational potential energy is

`U = -G(mM)/(r)=-(6.67\cdot 10^(-11))((525 kg)(5.98\cdot 10^(24)kg))/(6.37\cdot 10^6 m)=-3.29\cdot 10^(10) J`

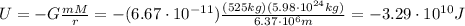
And since it hits the ground with speed

`v=1.90 km/s = 1900 m/s`

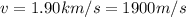
it also has kinetic energy:

`K=(1)/(2)mv^2=(1)/(2)(525 kg)(1900 m/s)^2=9.48\cdot 10^8 J`

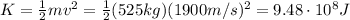
So the total energy when the satellite hits the ground is

`E_f = U+K=-3.29\cdot 10^(10)J+9.48\cdot 10^8 J=-3.20\cdot 10^(10) J`

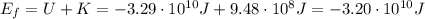
So the energy transformed into internal energy due to air friction is the difference between the total initial energy and the total final energy of the satellite:

`\Delta E=E_i-E_f=-1.51\cdot 10^(10) J-(-3.20\cdot 10^(10) J)=1.69\cdot 10^(10)J`