Answer:

Explanation:
To find out oblique asymptote we divide the polynomials using long division
To find quotient divide the first term. then multiply the answer with 3x+5 and write it down. Subtract it from the top. Repeat the process till we get remainder.
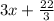
------------------------------
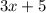
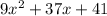

-------------------------------------(Subtract)

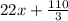
------------------------------------(subtract)

Quotient is
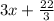 that is our oblique asympotote
that is our oblique asympotote
the value of k is 22/3