For this case we have that the figure shown is composed of a cylinder and a cone.
We have that the volume of a cylinder is given by:

Where:
A: It's the radio
h: It's the height
Substituting the values:
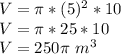
On the other hand, the volume of a cone is given by:
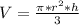
Where:
A: It's the radio
h: It's the height
Substituting the values:
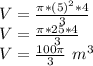
Then, the total volume is:
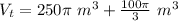
Taking
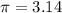 , we have to:
, we have to:
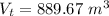
Answer:
Option D