Question

Use the following half-life graph to answer the following question:

A graph titled half-life graph of a radioactive isotope is shown with mass remaining on the y axis from 0 to 60 grams and time on the x axis from o to 6 minutes. A curve connects the points 0, 50 and 1, 25 and 2, 12.5 and 3, 6.25 and 4, 3.125 and 5, 1.5625.

The graph is attached.

What is the half-life of the isotope? (5 points)


A. 1.0 min

B. 3.0 min

C. 5.0 min

D. 6.0 min

Answer 1

A 1.0 min

Step-by-step explanation:

The half-life of a radioisotope is defined as the time it takes for the mass of the isotope to halve compared to the initial value.

From the graph in the problem, we see that the initial mass of the isotope at time t=0 is

`m_0 = 50.0 g`

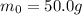
The half-life of the isotope is the time it takes for half the mass of the sample to decay, so it is the time t at which the mass will be halved:

`m'=(50.0 g)/(2)=25.0 g`

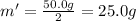
We see that this occurs at t = 1.0 min, so the half-life of the isotope is exactly 1.0 min.