P(A) = 0.40 P(B) = 0.50 P(A and B) = 0.10 What is P(B/A)

Question

asked Jun 16, 2020 39.4k views

2 Answers

JkShaw · Answer 1 · 2020-06-22T13:08:02+0000

Answer:

Final answer is
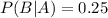P(B|A) = 0.25 .

Explanation:

We have been given values of

P(A) = 0.40, P(B) = 0.50, and P(A and B) = 0.10

Now we need to find about what is the value of P(B/A).

Apply formula
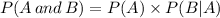
$P (A \, and \, B)=P(A) * P(B|A)$

Plug the given values into above formula:

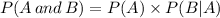
$P (A \, and \, B)=P(A) * P(B|A)$

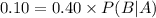
0.10 =0.40 * P(B|A)

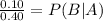
(0.10)/(0.40) =P(B|A)

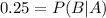
0.25 =P(B|A)

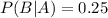
P(B|A) = 0.25

Hence final answer is
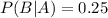P(B|A) = 0.25 .