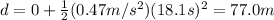9) 1.55 rad/s^2
The angular acceleration of the disk is given by
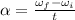
where
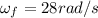 is the final angular speed
is the final angular speed
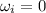 is the initial angular speed (the disk starts from rest)
is the initial angular speed (the disk starts from rest)
t = 18.1 s is the time interval
Substituting into the equation, we find:
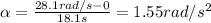
10) 253.9 rad
The angular displacement of the disk during this time interval is given by the equation:
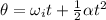
where
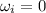 is the initial angular speed (the disk starts from rest)
is the initial angular speed (the disk starts from rest)
t = 18.1 s is the time interval
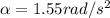 is the angular acceleration
is the angular acceleration
Substituting into the equation, we find:
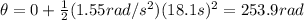
11)
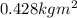
The moment of inertia of a disk rotating about its axis is given by
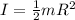
where in this case we have
m = 9.5 kg is the mass of the disk
R = 0.3 m is the radius of the disk
Substituting numbers into the equation, we find
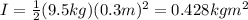
12) 167.8 J
The rotational energy of the disk is given by
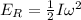
where
 is the moment of inertia
is the moment of inertia
 is the angular speed
is the angular speed
At the beginning,
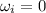 , so the rotational energy is
, so the rotational energy is
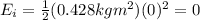
While at the end, the angular speed is
 , so the rotational energy is
, so the rotational energy is

So, the change in rotational energy of the disk is
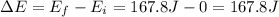
13)
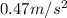
The tangential acceleration can be found by using
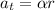
where
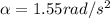 is the angular acceleration
is the angular acceleration
r is the distance of the point from the centre of the disk; since the point is on the rim,
r = R = 0.3 m
So the tangential acceleration is
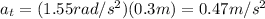
14)
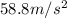
The radial (centripetal acceleration) is given by
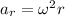
where
 is the angular speed, which is half of its final value, so
is the angular speed, which is half of its final value, so
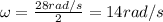
r is the distance of the point from the centre (as before, r = R = 0.3 m)
Substituting numbers into the equation,
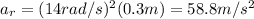
15) 4.2 m/s
The tangential speed is given by:
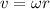
where
 is the angular speed
is the angular speed
r is the distance of the point from the centre of the disk, so since the point is half-way between the centre of the disk and the rim,
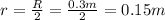
So the tangential speed is
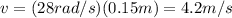
16) 77.0 m
The total distance travelled by a point on the rim of the disk is
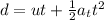
where
u = 0 is the initial tangential speed
t = 18.1 s is the time
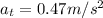 is the tangential acceleration
is the tangential acceleration
Substituting into the equation, we find