Question

Polygon Y is a scaled copy of Polygon X using a scale factor of \dfrac13 3 1 ​ start fraction, 1, divided by, 3, end fraction. Polygon Y's area is what fraction of Polygon XXX's area?

Answer 1

1/9

Explanation:

Answer 2

Polygon Y's area is one ninth (1/9) of Polygon X's area

Explanation:

we know that

If two figures are similar, then the ratio of its areas is equal to the scale factor squared

In this problem

Let

z-----> the scale factor

a-----> Polygon Y's area

b----> Polygon X's area

`z^(2)=(a)/(b)`

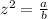
we have

`z=(1)/(3)`

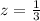
substitute

`((1)/(3))^(2)=(a)/(b)`

`(1)/(9)=(a)/(b)`

`a=(1)/(9)b`

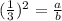
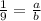
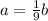
therefore

Polygon Y's area is one ninth (1/9) of Polygon X's area