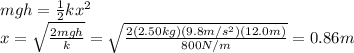Question

A 2.50 kg flower pot is pushed out a window this is at a height of 12.0m onto a spring with a spring constant of 800.N/m. How much does the spring compress if the ball comes to a stop.

Answer 1

0.86 m

Step-by-step explanation:

We can solve the problem by using the law of conservation of energy.

The initial mechanical energy of the flower pot is just gravitational potential energy, given by:

`E_i = U = mgh`

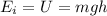
where

m = 2.50 kg is the mass of the pot

g = 9.8 m/s^2 is the acceleration due to gravity

h = 12.0 m is the height

When the pot hits and compresses the spring coming to a stop, all this energy is converted into elastic potential energy of the spring:

`E_f = U = (1)/(2)kx^2`

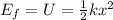
where

k = 800 N/m is the spring constant

x is the compression of the spring

Due to the conservation of energy,

`E_i = E_f`

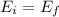
So we can write

`mgh=(1)/(2)kx^2\\x=\sqrt{(2mgh)/(k)}=\sqrt{(2(2.50 kg)(9.8 m/s^2)(12.0 m))/(800 N/m)}=0.86 m`