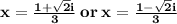Answer:
Solving the expression
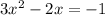 we get:
we get:
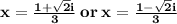
Explanation:
We need to solve the expression:
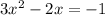
This is a quadratic expression and it can be solved using quadratic formula
Solving:
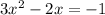
we can write it as:
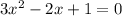
The quadratic formula is:
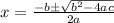
where a = 3, b = -2 and c= 1
Putting values and solving:

So, solving the expression
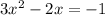 we get:
we get: