(a) 0.028 rad
The angular separation of the nth-maximum from the central maximum in a diffraction from two slits is given by
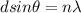
where
d is the distance between the two slits
 is the angular separation
is the angular separation
n is the order of the maximum
 is the wavelength
is the wavelength
In this problem,
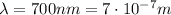
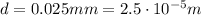
The maximum adjacent to the central maximum is the one with n=1, so substituting into the formula we find
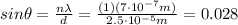
So the angular separation in radians is
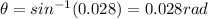
(b) 0.028 m
The screen is located 1 m from the slits:
D = 1 m
The distance of the screen from the slits, D, and the separation between the two adjacent maxima on the screen (let's call it y) form a right triangle, so we can write the following relationship:
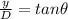
And so we can find y:
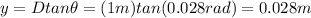
(c)
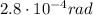
In this case, we can apply again the formula used in part a), but this time the separation between the slits is

so we find

And so we find
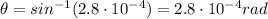
(d)
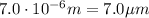
This part can be solved exactly as part b), but this time the distance of the screen from the slits is
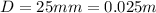
So we find
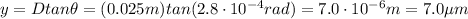
(e) The maxima will be shifted, but the separation would remain the same
In this situation, the waves emitted by one of the slits are shifted by
 (which corresponds to half a cycle, so half wavelength) with respect to the waves emitted by the other slit.
(which corresponds to half a cycle, so half wavelength) with respect to the waves emitted by the other slit.
This means that the points where previously there was constructive interference (the maxima on the screen) will now be points of destructive interference (dark fringes); on the contrary, the points where there was destructive interference before (dark fringes) will now be points of maxima (bright fringes). Therefore, all the maxima will be shifted.
However, the separation between two adjacent maxima will not change. In fact, tall the maxima will change location exactly by the same amount; therefore, their relative distance will remain the same.