Question

Suppose that we wish to assess whether more than 60 percent of all U.S. households in a particular income class bought life insurance last year. That is, we wish to assess whether p, the proportion of all U.S. households in the income class that bought life insurance last year, exceeds .60. Assume that an insurance survey is based on 1,000 randomly selected U.S. households in the income class and that 640 of these households bought life insurance last year

Answer 1

dont know

Explanation:

Answer 2

Explanation:

Set up hypotheses as:

`H-0: p=0.60\\H_a: p >0.60`

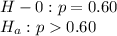
(Right tailed test)

Sample proportion p = favourable/total =
`(640)/(1000) =0.64`

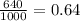
p difference
`=0.64-0.60 =0.04`

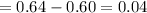
Sample std error =
`\sqrt{(pq)/(n) } =\sqrt{(0.64(0.36))/(1000) } \\=0.0152`

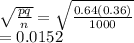
Critical value for95% = 1.96

Margin of error =
`1.96(0.0152)\\= 0.0298`

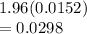
Confidence interval for proportions

=
`(0.64-0.0298, 0.64+0.0298)\\=(0.6102,0.6698)`

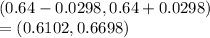
Since confidence interval does not contain 0.60 we reject null hypothesis.

At 5% significance level we can accept thta proportion >0.60